Note: this is adapted from a paper I wrote for a technical writing class.

Table of Contents

Introduction
A Baseline for Abstraction
Direct Relationship with Undergraduate Math
Category Theory in the History of Math
Professional Opinions on Category Theory
An Example for Calculus Students
Conclusion
Appendices
Works Cited

Introduction

Math courses use memorization of calculations, theorems, lemmas, and corollaries, but category theory offers a way to study math holistically and intuitively. Category theory is the study of abstract mathematical structures as opposed to the memorization of formulas. Categories in math are analogous to the setting of a story. Just like every story has a protagonist, categories all have objects. The object is different in each category. An introduction to category theory for STEM undergraduates needs a balance of vernacular with complexity and abstraction. Understanding how math works is usually reserved for Ph.D. students but undergraduate students could learn some of these principles to understand and apply the principles of math. This raises the problem: how can an undergraduate course use category theory to reduce the required memorization without obscuring course material in abstraction? The development of category theory as a discipline, the history of mathematical research, and examples from mathematical practice illustrate the potential for an undergraduate course in category theory even while categorical treatment of these subjects falls back on multiple layers of abstraction.

A Baseline for Abstraction

A popular case in the mathematics community is “Why can you turn clothing right-side-out?”, the highest scoring question under topology on Mathematics Stack Exchange (Abichandani).¹ In this case, the highest-scoring mathematical response touched largely on manifold theory and algebraic topology.² But, the questioner accepted the second highest-scoring response as the answer despite its using minimal math. This is because it is easy to get lost in abstraction. The contrast between discussing the “homotopy long exact sequence of a fibration” and sewing pants cuffs together highlights the difficulty with category theory (“CT”).

This raises the question: how far should an undergraduate course go to balance understanding abstract concepts of CT without losing sight of the undergraduate math concepts? To understand the benefits of an undergraduate course in CT, it is crucial to know the level of complexity such a course would build up to. According to Lawvere and Schanuel, to begin a study of CT a student must start with basic examples such as a set³ of colors {red, yellow, blue}. But sets are not immediately relevant to a calculus course. Further, most trivial examples of groups⁴—involve the integers rather than the real numbers⁵ which are preferred for calculus, matrix algebra, and differential equations.

To begin relating the basic examples of CT with conceptual math like calculus, introductory CT examples must be examined. The book Conceptual Mathematics solely works in the category of sets, where objects are sets and morphisms are arrows that represent changes between objects i.e. functions for sets.⁶ Begin with a silly example the “set of people” A={Bilbo, Sam, Gandalf, Frodo} has a morphism f= “favorite” to the “set of colors” B = {red, orange, yellow, green, blue} (Lawvere and Schanuel 14). Notice, the map here does not reverse, as at least one of the colors is not a favorite, so f : A → B is not an isomorphism.⁷ Meanwhile, the morphism f : A → A is isomorphic only if no two people have the same favorite person. This opens the door to calculus where isomorphism is a one-to-one function. This categorical view of isomorphism does not require the abstractions from GEH that Appendix A illustrates. It is everywhere in calculus, where such theorems as Rolle’s theorem, the extreme value theorem, and the fundamental theorem of calculus all require functions to be isomorphic (Kofman). Instead of having numerous definitions from an advanced course like topology, students can draw arrows between letters to illustrate the same mathematical concept.⁸ This is one benefit of implementing CT as part of undergraduate studies.

A second major motivation of CT is the composition of morphisms, which Figure 1 (Appendix B) illustrates in the connection between integrals and derivatives in calculus. Working with the examples from Conceptual Mathematics using sets, the equation f ∘ f: A → A → B gives the favorite color of each person’s favorite person where f is the “favorite morphism”, A is the “people set”, and B is the “color set” all in the category of sets. So, if Sam favors Bilbo, and Bilbo favors green, then this gives f ∘ f(Sam) = green for the morphism on these sets.

Now, the only two rules for composition, are associativity or grouping of operations:

f ∘ g ∘ h = (f∘g) ∘ h = f ∘ (g∘h)

and identity or sending the input to the output f ∘ f⁻¹: x → x. For example, as depicted in Figure 2 (Appendix B) let 𝑓₁ ⋅𝑓₂ ⋅𝑓₃ : A → A → A → A give “Gandalf favors Sam favors Bilbo favors Frodo”. We can find “Gandalf favors Sam favors Bilbo” first or “Sam favors Bilbo favors Frodo” first.⁹ For identity, simply put, if Gandalf favors Sam, and Sam’s favorer is Gandalf, we go in a full circle from Gandalf to Sam and back. While these are basic notions of CT, they apply to many mathematical concepts in calculus and other undergraduate math studies including objects such as sets, topological spaces, groups, rings, fields, manifolds, measure spaces, chain complexes, and field vector spaces with their appropriate morphisms (Riehl 5).¹⁰

Beyond these basic definitions of morphisms and objects (arrows and letters), CT develops more advanced ideas relevant to undergraduate math students. However, for the purpose of drawing immediate connections between CT and calculus, morphisms and objects are sufficient.¹¹ After considering the history of mathematics and professional opinions on category theory, the ideas of objects and isomorphism illustrated above provide a basic idea of how category theory can help undergraduates in calculus.

Direct Relationship with Undergraduate Math

The problem is that CT immediately relates to elementary calculus, matrix algebra, and differential equations in a “trickle-down” manner. Category theory is a setting for mathematics, especially drawing connections between algebra and topology or geometry—much how pythogoras described a right triangle’s sides as a² + b² = c² (Lawvere and Schanuel xiii). Appendix A demonstrates how far away the category theory of group extensions and homology are from undergraduate math.¹² While developing the topology of these group extensions relates to category theory, it falls into the same errors as the popular explanation for turning clothes right-side out, lost in abstraction.

Category Theory in the History of Math

Undergraduates benefit from studying CT today because it is the culmination of unifying theories in the history of mathematics. Two revolutions in the breadth of mathematics occurred during the twentieth sources that set all fields of study in the direction of CT. First, in 1900, at the International Congress of Mathematicians in Paris, David Hilbert proposed his project for an axiomatic foundation to unify all of mathematics using logic, a project that was successful over the course of the twentieth century, and second, the Nicholas Bourbaki group worked in France from the 1930s to the 1980s to develop a rigorous axiomatic treatment of mathematical subjects, a treatment that does not rely on applied application and thus solidifies mathematics as not only purely logical but also as a stand-alone abstract structure that does not rely on the disparate forays of historical thinkers in number games (Dyson 213). The drawback of these initial formalizations is that they do not allow for the playful experimentations that CT now allows for:

Any rigorous foundation capable of supporting the ordinary theory of classes would equally well support our theory…leaving the reader free to insert whatever type of logical foundation (or absence thereof) he may prefer (Eilenberg and Mac Lane, “General Theory…”, 246)

As Dyson recalls, imaginary numbers¹³ were a purely elegant, artistic theory for thinkers from Bernhard Riemann and Karl Weierstrass back to Niels Henrik Abel in the 1800s, which after a century, Erwin’s Schroediger used by intuition for his uncertainty principle in quantum mechanics (213). CT is a central area for researching these broad and unifying mathematical concepts today, for which Hilbert and Bourbaki’s work is sufficient but not necessary. It works in tandem with mathematical research done at a more exact, detailed level, done by mathematicians whom Freeman Dyson terms “frogs” in contrast with the “birds” such as Schroedinger. That is, CT provides a pre-packaged birdseye view for anyone to employ—especially frogs in undergraduate engineering, medicine, etcetera.

The role of CT as a birdseye view evolved from the work of Samuel Eilenberg and Saunders Mac Lane. However, as seen in Appendix A, an overview of CT’s beginning demonstrates why critics of CT dismiss the field with such claims as Antoni Zygmund’s: “take a centipede and pull off ninety-nine of its legs and see what it can do” (Krantz 6). That is, every algebraic structure is a mutilated form of some previous one, removing a requirement, as illustrated in Figure 3 (Appendix B). All these new nouns raise the same memorization issue as do theorems, lemmas, and corollaries. Appendix A thus demonstrates that group theory and for a calculus student is just a centipede with only a few legs left, and Figure 3 suggests the problems that centipede math poses for memorization. While Dyson outlines the necessity for both birds and frogs in his speech, the practices for science and engineering classes are largely calculations and computations (Belk) that are more suitable to the case of frogs.

Professional Opinions on Category Theory

Professor Eugenia Cheng’s Joy of Abstraction demonstrates how category theory applies to many areas of life, even social justice issues. She moves from a general philosophical discussion about topics such as patterns and relationships to examples of mathematical objects, even defining grandmothers as compositions of mother morphisms (101). But, by the time Cheng reaches the Yoneda Lemma her prose does not differ much from many textbooks (366).¹⁴ Nonetheless, this does not suggest the Yoneda Lemma is out of reach for a general audience so much as it suggests a more general idea in math, that understanding requires examples, as with adjoint functors (Lumsdale). Cheng’s more philosophical insights suggest how undergraduates can use category theory, as it provides a framework for understanding and organizing complex systems.

Cheng highlights that CT focuses on the relationships between objects rather than on the objects themselves. She says, “In basic category theory our insight begins by saying we should study relationships between objects, not just the objects themselves” (21). This approach is helpful in STEM fields, where different elements of systems interact with each other in chemistry, biology, physics, and computing. Cheng even suggests that CT provides a common language and framework that applies to a wide range of fields because it “makes connections between diverse situations to help us unify them and think about them more efficiently” (2). This means that students can develop skills that transfer across different disciplines, which is useful in STEM fields where interdisciplinary collaboration is becoming increasingly important.

Still, mathematics in general fits these claims. As to what sets CT apart, Cheng further argues that, “Sometimes category theory can feel like arbitrary abstractions for the sake of it; in that case I think something is missing” (397). By providing a way to abstract away from specific details and focus on the relationships between objects, category theory can help students to see the big picture and to identify underlying patterns and structures. By focusing on relationships rather than individual objects, providing a common language across disciplines, and helping to identify patterns and structures, category theory can help with understanding and analyzing complex systems.

An Example for Calculus Students

With this history in mind a further motivating example is something a calculus student might notice: that differentiation undoes integration, but integration does not undo differentiation. The exploration of the CT behind this observation is more abstract than anyone who has not taken calculus can appreciate, but it solely employs the ideas students learn in derivative and integral calculus classes. Thus for a layperson, this example faces the same issue as the topology of clothes folding, but a calculus student has all the tools necessary to benefit from the example.¹⁵ First, consider the case of the Fundamental Theorem of Calculus:¹⁶

\(\frac{d}{dx}f(x)dx \neq \frac{d}{dx}f(x)dx\)

Now, to illustrate, let f(x) = x which defines \(f(x)dx = \frac{x^{2}}{2} + C\) and also \(\ \frac{d}{dx}f(x) = 1\), which gives

\(\frac{d}{dx}(\frac{x^{2}}{2} + C) \neq 1dx\)

x + 0 ≠ x + C

This is only true if C = 0, which is not guaranteed for antiderivatives or indefinite integrals. This is not of concern for classical mechanics in physics—where the position is the integral of velocity, which is the integral of the acceleration all with respect to time—because an accelerating object generally has a starting position and velocity. For example, a car usually starts parked at someone’s house before it starts speeding up on the highway. Similarly, in finance, investments start with a certain value before increasing or decreasing at different rates. But, CT illustrates this with the commutative diagrams in Figure 2 (Appendix B).

To allow this isomorphism to be natural as GEH defines, one must not choose C=0, which is where the centipede comes in.¹⁷ Meanwhile, there exist no elementary integrals that send elementary functions to zero in this sense. Since it is so complicated to make this isomorphism natural, in this example might call the derivative a left adjoint that “forgets” constants, while the integral is a right adjoint that “remembers” constants. This is the same as having more possible favorite colors than there are people.¹⁸ Even the details of this example from calculus that treats first-year calculus with little more than morphisms verges on too much abstraction. But, readers who know category theory before calculus or linear algebra can get a gist of how derivatives and integrals relate by knowing that they are left and right adjoint functors without the symbolic mess of C^∞(ℝ) and ∫𝑓(x)dx and d𝑓/dx.

Conclusion

Beyond this example in calculus, CT is applicable in other fields which would also be helpful to undergrads. Researchers in linguistics have used CT. They use morphisms between morphisms (arrows between arrows or higher order relationships showing connections) among different types of plural nouns such as a lot of coffee vs many coffees (La Palme, et al). Others have used category-theoretic concepts such as co-limits and higher algebras to describe structures, processes, and so-called “processes of processes” in neuroscience (Brown and Porter). Further still, the composition of functions in programming languages such as Haskell requires the use of morphisms, functors, and natural transformation to allow for transparency and optimization of concurrent, large-scale computer programming designs (Milewski). The development of category theory as a discipline, the history of mathematical research, and examples from mathematical practice illustrate the potential for an undergraduate course in category theory even while categorical treatment of these subjects falls back on multiple layers of abstraction. Students can then go on to apply categorical principles to any area of study to help them understand the “whys” and “hows” in their fields of study.

Word Count: 2474

Appendices

Appendix A

For readers interested in attempting the jump to group theory, such a jump illustrates how category theory can obscure math behind abstraction, and how far the fields of group theory and algebraic topology are from typical classes taken by STEM undergraduates. Appendix A is completely optional in relating CT to undergraduate math. The motivation for this appendix was to illuminate the structure of these functions the positive real numbers R⁺, even to the point where a student can begin to form an intuition for why Riehl claims “the chain rule expresses the [so-called] functoriality of the derivative” (Riehl 14). The construction of other sets of numbers following the real numbers is elementary—the rational numbers or fractions:

Q = { n, q, d, ∈ R | n = qd + r , d ≠ 0, r = 0}

the integers:

Z = { n, q, d, ∈ R | n = qd + r , d ≠ 0, r = 0, n = d}

and the complex numbers:

C = {x + iy | x, y ∈ R and i = }

These definitions from elementary mathematics are a first step in clarifying the obscure beginnings of category, the very obscurity which prevents wider appreciation of CT today.

A general notion of the conception of categorical ideas from Eilenberg and Mac Lane’s seminal paper Group Extensions and Homology (“GEH”) requires a background in group theory or algebraic topology. Formal homology¹⁹ is the topic of GEH, but according to Bradley, it is beyond the scope of even an undergraduate topology course (Bradley et al. x).

An example of how an undergraduate course might get lost in abstraction lies in an attempt at an intuitive preview of GEH, a paper that introduces the motivation behind CT but makes no mention of the terms category, morphism, or functor, as the duo introduced these terms three years later in their paper “General Theory of Natural Equivalences” (EM). Rather the earlier paper outlines what is now known as the natural transformation.²⁰ The specific topics of this first paper employ abstract algebra and topology. Still, intuitive definitions can peak a student’s interest and set the course for future study. For example, the advanced notion of homology identifies mathematically unchanging properties called invariants in topology that can are intuitively holes or emptiness in shapes—the common joke being topologists cannot distinguish donuts from coffee cups, both having one hole. Now, EM’s use of group extensions to define the relationship between homology and cohomology in topological groups is more intricate than the general notion of homology (EM, “Group…”, 769). Even though this notion is more intricate, it is still crucial to the original motivations for CT that are found in the paper.

Without getting into the minutiae of EM’s employment of abstract algebra in homology theory, begin by considering the group extension. To start, group extensions provide a trivial construction of a direct product (Idem. 767)—which high school algebra exemplifies by using the the real numbers R as a horizontal line x and vertical line y to give the coordinates (x,y), or {x, y ∈ R | (x,y) ∈ R × R }. The result of this construction is familiar to any elementary algebra student, acting as another detail to motivate the wider practice of CT.

An undergraduate course in category theory that mediates abstraction can employ simple definitions from group theory. The direct product arises because a subgroup G which also forms a factor group H = E/G of the group E forms an extension of G by H (Idem 767). The trivial form can also be succinctly written in the more contemporary form that Saunders Mac Lane uses in his expository paper from 1999: 0 → G → G × H → H → 0 where E = H × G (Mac Lane 128). That is, G represents a normal subgroup—meaning its elements g ∈ G can be composed with the elements x, x⁻¹ ∈ E such that xgx⁻¹ ∈ G— or trivially, for all g ∈ (Z,+), the element of the singleton set g ∈ {g} satisfies x, x⁻¹ ∈ (Z,+) such that xgx⁻¹ ∈ {g}, for example letting x = 2, x⁻¹ = ˗2 , and {g} = {1} where 1 + 1+ (−1) = 1 ∈ {1}. Now a factor group also called a quotient group—which the group of odd integers exemplifies as the quotient group of the integers with the even integers Z/2Z. Further, a quotient group H is only a free group—which the group of integers under addition (Z,+) exemplifies since its underlying set only contains the number 1, or intuitively, any integer can be expressed as a sum or difference of ones—if any extension by H is the trivial extension, or the direct product (Idem. 767). Of course, these definitions are in the field of study labeled abstract algebra, not strictly CT, but the latter is what ties these ideas into the larger picture of mathematics.

The final piece of the puzzle for this part of GEH is the transformation group, which EM constructs precisely to show the linear or “affine” nature—intuitively, squashability and slide-ability—of this group over the set of invertible functions (EM, “Group…”, 768). But for the general reader, this group is exemplified in a simple principle: the transformation group for translations in Euclidian space, which is the space where high school math happens and is represented by (x,y) ∈ R × R, allow that a circle of a fixed radius has the same properties no matter where it is positioned, sliding vertically or horizontally in any order any number of times (Joyce).

These group definitions in the context of GEH are enough to explain the first method learned in an integral calculus class: substitution. Consider the group extension that correlates to the quadratic function seen in elementary algebra and calculus courses. Let a ⋅ b be multiplication, (a,b) ∈ A × B be a direct product, y ∈ R⁺ be R > 0, R_≠ 0be x ∈ R ≠ 0. Now, 1 → (R_≠ 0,⋅) → (R_≠ 0×R⁺,⋅) → (R⁺,⋅) → 1. Where H = (R_≠ 0,⋅), G = (R_≠ 0×R⁺,⋅), and G/H = (R⁺,⋅), so G extends G/H by H. This defines the equation y = x², but notice this does not satisfy = = x because y > 0 cannot give x < 0, so (˗x,y)∉ R_≠ 0 × R⁺, which is false. The group extension for the underlying set R_≠ 0 × R⁺ does not demonstrate the isomorphism (, y) ≅ (x, y²). Thus, to see EM’s full power considers the case where (R⁺,⋅) extends itself, in turn allowing for the transformation group which is essential to GEH.

Let H = (R⁺,⋅), G × H = (R⁺×R⁺,⋅), and (G×H)/H = (R⁺,⋅):

1 → (R⁺,⋅) → (R⁺×R⁺,⋅) → (R⁺,⋅) → 1

for which two relations satisfy y=: (x, y²), (, y) ∈ R⁺ × R⁺ But further, the group (R⁺×R⁺,⋅) being closed under multiplication also gives (x²ⁿ, yⁿ) ∈ R⁺ × R⁺ for n ∈ Q. This example also satisfies the definition (EM 768) of a transformation group T ∋ t for group G ∋ g(h), g(k) with normal subgroup H ∋ h, k that satisfies the function

t(h,k) = g(h) ∘ g(k) ∘ g⁻¹(h∘k)

as trivially the identity under multiplication such that \(1 = \ \frac{\sqrt{h} \cdot \sqrt{k}}{\sqrt{h \cdot k}}\ \) which, further, proves a natural transformation for all possible extensions of R⁺by R⁺ given EM’s next step.

With all of this intricate detail aside, the group extension relates to topology through a meta feat of mathematical acrobatics. The topology comes from the group formed from the sets of extensions for H in G, called Ext {G, H} that is the quotient of the group of the factor sets Fact {G, H} and the group of the transformation sets Trans {G, H} of H in G (EM, “Group”, 770). That is

Ext {G, H} = Fact {G, H}/Trans {G, H} .

Note that the example on R⁺ requires the exploration of function spaces formed by the set of functions that makes up Fact {G, H} and Trans {G, H}.²¹ Before taking advantage of the topology that arises here, EM relates extensions to homomorphisms. These change one group into another and are considered as a synonym for functions, transformations, and arrows (Lawvere and Schanuel 14, Riehl xi). EM takes several pages proving that a factor set or a homomorphism into G from R gives an extension by H of G, if H = F/R the normal subgroup is itself a factor group of F a free group and some group R, then

Ext {G, H} ≅ Hom {R, G}/Hom {F|R, G}

where ≅ denotes an isomorphism, and this expression as a whole is now deemed a natural transformation which EM applies to homology and cohomology (EM, “Group”, 772). At this point, the reader can see categorical notions emerge as the isomorphism between the set of homomorphisms of some groups illustrates the notion of what is now known as a functor between categories, and the authors go on to prove a natural transformation through the existence of morphisms between all of these functors (Idem. 775). This lays out a view of the layers of abstraction at the heart of CT’s origin, a motivation for the subject’s conception which can even stretch to the subjects applications in more applied areas today.

Appendix B

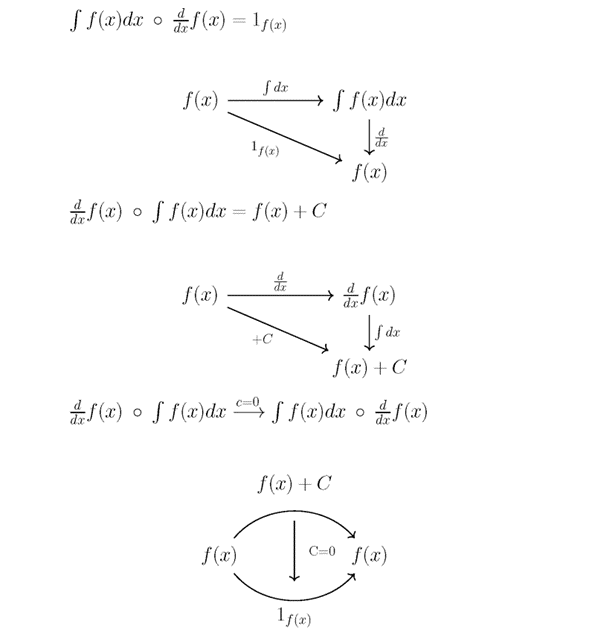
Figure 1: There is a superficial adjunction between the left and right compositions of integration and differentiation, meaning they require a morphism (change) to form an identity (a change from something back to itself), but these commutative diagrams lack algebraic structure (centipede mathematics) for the functions. Source: Izak Schmidlkofer, Feb 2023

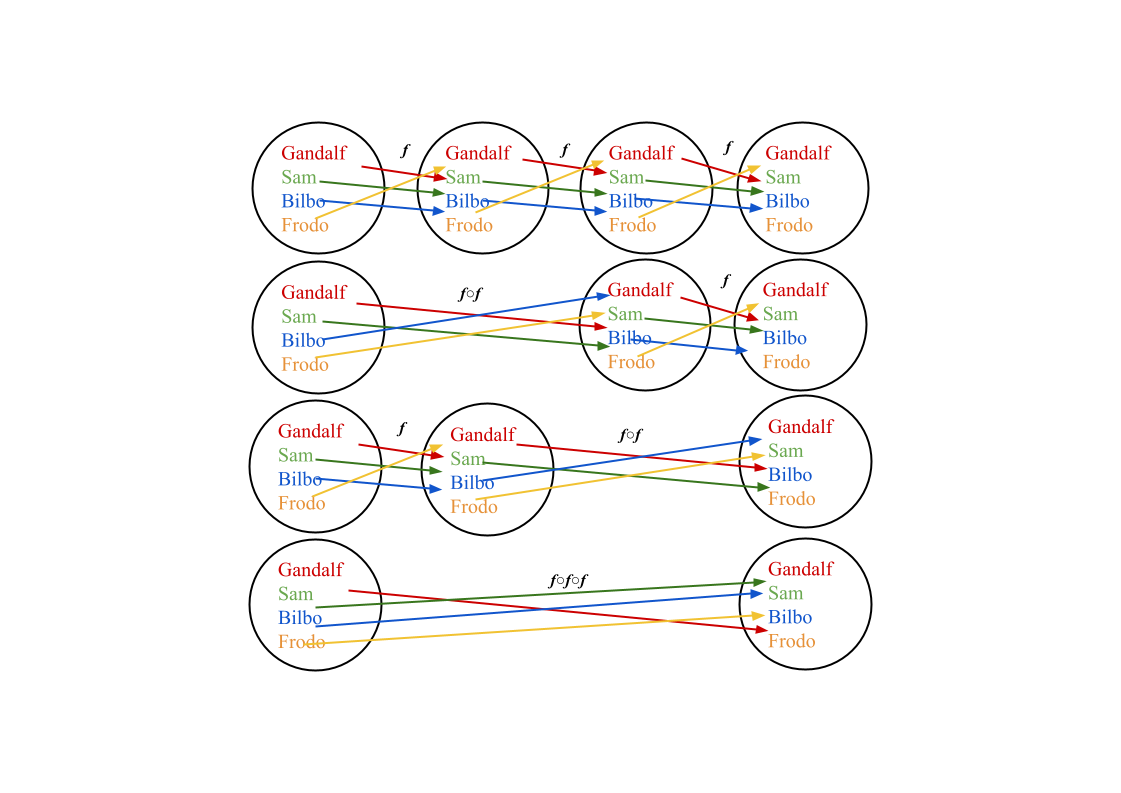
Figure 2. The trivial example of associativity among morphisms between sets generalizes to associativity in group-like objects, where the motivation for CT emerges from group extensions in GEH as the appendix begins to demonstrate for R⁺ × R⁺under multiplication.

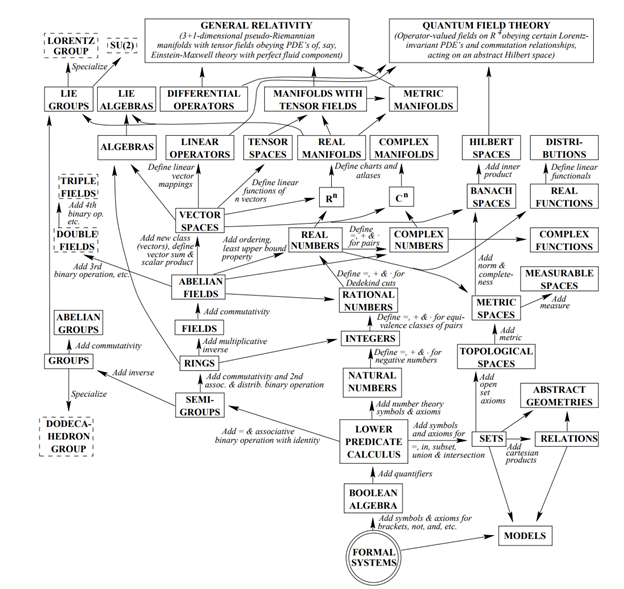
Figure 3 This diagram from a physics journal article (Source: Max Tegmark, 1998) illustrates so-called centipede mathematics, where category theory would occupy two positions: on a similar level as sets, and as a means for tearing off the centipede’s legs—drawing arrows between the boxes.

Appendix C

Further Reading

Bradley, Tai-Danae. “What is an Adjunction? Part 1 (Motivation).” Math3ma: Categories. 19

Sep 2019, Accessed 14 Feb 2023.

https://www.math3ma.com/blog/what-is-an-adjunction-part-1

——— “What is a Category? Definition and Examples.” Math3ma: Categories. 23 Jan 2017,

Accessed 14 Feb 2023. https://www.math3ma.com/blog/what-is-a-category

——— “What is a Functor? Definition and Examples, Part 1.” Math3ma: Categories. 31 Jan

2017, Accessed 14 Feb 2023. https://www.math3ma.com/blog/what-is-a-functor-part-1

——— “What is a Functor? Definitions and Examples, Part 2.” Math3ma: Categories. 2 Feb

2017, Accessed 14 Feb 2023. https://www.math3ma.com/blog/what-is-a-functor-part-2

——— “What is a Natural Transformation? Definition and Examples.” Math3ma: Categories. 7

Feb 2017, Accessed 14 Feb 2023.

https://www.math3ma.com/blog/what-is-a-natural-transformation

Holden, David. “Corresponding Isomorphism Real Number.” Mathematics Stack Exchange. 8

Dec 2013. Accessed 10 Mar 2023. https://math.stackexchange.com/a/597965/1098426

Ikenaga, Bruce. “Direct Products.” Abstract Algebra 1. Millersville University. 2 Mar 2018,

Accessed 8 Mar 2023. https://sites.millersville.edu/bikenaga/abstract-algebra-1/product/product.pdf

——— “First Isomorphism Theorem.” Abstract Algebra 1. Millersville University. 22 Mar 2018,

Accessed 8 Mar 2023. https://sites.millersville.edu/bikenaga/abstract-algebra-1/first-isomorphism-theorem/first-isomorphism-theorem.pdf

——— “Group Homomorphisms.” Abstract Algebra 1. Millersville University. 17 Jan 2018,

Accessed 8 Mar 2023. https://sites.millersville.edu/bikenaga/abstract-algebra-1/group-maps/group-maps.pdf

——— “Normal Subgroups and Quotient Groups.” Abstract Algebra 1. Millersville University.

17 Mar 2018, Accessed 8 Mar 2023.

https://sites.millersville.edu/bikenaga/abstract-algebra-1/normal-subgroups/normal-subgroups.pdf

Karagila, Asaf. “Basis for R Over Q.” Mathematics Stack Exchange, 24 Feb 2012, Accessed 10

Mar. 2023. https://math.stackexchange.com/a/112867/1098426

——— “What Is Aut(R,+)?” Mathematics Stack Exchange, Mar. 2012, Accessed 10 Mar.

2023. https://math.stackexchange.com/a/115688/1098426

Samuel, Matthew. “Automorphism Group of (R^⨉,·).” Mathematics Stack Exchange. 23 Feb 2019,

Accessed 10 Mar 2023, https://math.stackexchange.com/a/3123607/1098426

Thurston, William. “On Proof and Progress in Mathematics.” Bulletin of the American

Mathematical Society, vol. 30, no. 2, 1 Jan. 1994, pp. 161–178, https://doi.org/10.1090/s0273-0979-1994-00502-6.

‌

Works Cited

Abichandani, Christopher. “Why Can You Turn Clothing Right-Side-Out?” Mathematics Stack

Exchange. 19 Aug 2010. https://math.stackexchange.com/q/2755/1098426

Belk, James. “How much memorization should be required in a first-semester calculus course?”

Mathematics Educators Stack Exchange. 31 Mar 2014. Accessed 28 February 2022. https://matheducators.stackexchange.com/a/1080

Bradley, Tai-Danae, et al. Topology: A Categorical Approach. Massachusetts Institute of

Technology Press, 2020, https://topology.mitpress.mit.edu/.

Brown, Ronald, and Timothy Porter. “Category Theory and Higher Dimensional Algebra:

Potential Descriptive Tools in Neuroscience.” Mathematics: Category Theory. Arxiv, Feb 2008. https://arxiv.org/PS_cache/math/pdf/0306/0306223v1.pdf
Cheng, Eugenia. The Joy of Abstraction. Cambridge University Press, 2022.

Dyson, Freeman. “Birds and Frogs.” Notices of the AMS. American Mathematical

Society. Vol 56, No 2. Feb 2009. pp. 212-223.

Eilenberg, Samuel, and Saunders Mac Lane. “General Theory of Natural Equivalences.”

Transactions of the American Mathematical Society, vol. 58, no. 2, 1945, pp. 231–94. JSTOR, https://doi.org/10.2307/1990284. Accessed 26 Feb. 2023.

———. “Group Extensions and Homology.” Annals of Mathematics, vol. 43, no. 4, 1942, pp.

757–831. JSTOR, https://doi.org/10.2307/1968966. Accessed 26 Feb. 2023.

Joyce, David. “Transformation Groups.” Modern Algebra. Clark University. 2003. Accessed 26

Feb 2023. http://aleph0.clarku.edu/~djoyce/modalg/transgroups.html.

Kofman, Ilya. “Calculus Formulas.” Calculus II. City University of New York. Accessed 26

February 2023. https://www.math.csi.cuny.edu/~ikofman/calculus_formulas.pdf

Krantz, Steven. Mathematical Apocrypha Redux: More Stories and Anecdotes of Mathematicians

and the Mathematical. Mathematical Association of America, 2005.

Lawvere, William, and Stephen Schanuel. Conceptual Mathematics: A First Introduction to

Categories. 2nd ed. Cambridge University Press, 2009.

La Palme Reyes, Marie, et al. “CountNouns, Mass Nouns and Their Transformations: a

Category-Theoretic Unified Semantics.” Language, Logic and Concepts. Bradford Book, MIT Press, 1999. pp 427-452. https://marieetgonzalo.files.wordpress.com/1999/06/mnmac1.pdf

Logan, Matthew. “Why arent integration and differentiation inverses of each other?”

Mathematics Stack Exchange. 27 Dec 2014. Accessed 28 Feb 2023. https://math.stackexchange.com/a/1082248/1098426

Lumsdale, Peter. “In Category Theory Why Is a Right Adjoint Not a Left Adjoint?” Mathematics

Stack Exchange, 22 Nov. 2011, Accessed 16 Mar 2023, https://math.stackexchange.com/a/84460/1098426

Mac Lane, Saunders. “Samuel Eilenberg and Categories.” Journal of Pure and Applied Algebra.

Vol 168, No 2. Elsevier Science, 2002. pp 127-131. https://doi.org/10.1016/S0022-4049(01)00092-5

Magidin, Arturo. “What is the transformation group of a direct product (trivial group

extension)?” Mathematics Stack Exchange. 28 Feb 2023. Accessed 28 Feb 2023. https://math.stackexchange.com/q/4648405/1098426

Milewski, Bartosz. “Category Theory for Programmers: The Preface.” Bartosz Milewskis

Programming Cafe: Category Theory, Haskell, Concurrency, C++. 28 Oct 2014. https://bartoszmilewski.com/2014/10/28/category-theory-for-programmers-the-preface/

Riehl, Emily. Category Theory in Context. Courier Dover Publications, 2016,

https://math.jhu.edu/~eriehl/context/.

Tegmark, Max. “Is ‘the theory of everything’ merely the ultimate ensemble theory?.” Annals of

Physics. Vol 270 No 1, 20 Nov 1998, pp 1-51. https://doi.org/10.1006/aphy.1998.5855

This relates to the “empty space” in a shape. For example, an inflatable bagel poked with a pin has three: the volume holding the air, the bagel hole, and the hole the needle pokes. This has the same shape as pants with the cuffs sewn together, and it cannot be turned inside out. Simply put, a shirt has no bagel hole despite having four needle holes, so it can turn inside out. Homology describes these hole with cycles and boundaries.↩︎
Manifold theory studies spaces that locally play by the rules of Euclid’s Elements. Algebraic topology studies how stretching and squishing preserve properties in shapes via abstract algebra—for structures see Figure 3 in the Appendix B.↩︎
Sets are lists with no order or repetitions, where elements x of the set S are x 𝜖 S↩︎
Groups are sets closed under an operation like addition, so adding any element to any other will only result in another element of the underlying set (See “Further Reading” in Appendix C).↩︎
Integers ℤ={...˗2, ˗1, 0, 1, 2...}and real numbers {1.543, ˗2, ½ , √3, 0} ⊂ ℝ↩︎
Functions take inputs and applu the same rule to each output—for example 𝑓(x) = x + 1 adds one to every possible x defined for 𝑓↩︎
Isomorphisms can be thought of as reversible maps, which division exemplifies when it “undoes” multiplication on the real, rational, and complex numbers.↩︎
These theorems obscure this fact behind topological terms such as continuity and smoothness which gain intuition in this categorical perspective of isomorphisms. Consider for example the definition: “A function 𝑓: X → Y between two topological spaces is continuous if and only if 𝑓^-1U is open in X whenever U is open in Y” (Bradley, et al. 3) which might deter general readers↩︎
More precisely, first find 𝑓₁⋅𝑓₂ that Gandalf favors Sam favors Bilbo and move on to find Bilbo’s favorite, or we can find 𝑓₂⋅𝑓₃ that Sam favors Bilbo favors Frodo and retroactively find that Gandalf favors Sam. In each case 𝑓 maps every person to the appropriate person, so no matter how we group 𝑓_n⋅𝑓_n+1 starting with any given person in a series of three favorites always gives the final favorite person.↩︎
See Figure 3 in the Appendix B. Also, Of these categories, those involving topological spaces, manifolds, and field vector spaces are of most interest to the undergraduate in calculus, matrix algebra, and differential equations, where morphisms are functions.↩︎
They include further concepts as functors or morphisms between categories, adjunction or left and right morphisms with the identity, natural isomorphism—or a morphism between functors, and the Yoneda Lemma or defining every mathematical structure by all morphisms to or from it (Riehl 13, 116, 24, 55). But an intuitive motivation for these ideas requires exploration of universal properties and duality, which leads to initial objects and terminal objects, and also pushouts and pullbacks. See Cheng (206-367)↩︎
Appendix A evaluates a real-valued group extension in relation to a few elementary functions, the latter of which many students learn in high school algebra and go on to study further in integral and differential calculus, but the process as a whole does not relate the group extension in algebraic topology to calculus through to category theory.↩︎
Imaginary numbers extend the real number line ℝ into a plane of complex numbers ℂ where where a + bi 𝜖 ℂ such that a, b 𝜖 ℝ and i² = -1.↩︎
For examples see books in the Works Cited such as Riehl’s Category Theory in Context and Bradley’s Topology: A Categorical Approach↩︎
For the layperson: in geometry, a derivative (called d𝑓 ⁄dx) gives the slope of a curve, and an integral (called ∫𝑓dx) gives the area under a curve. For a discussion of how to think about mathematical proofs and derivatives see Thurston in Appendix C.↩︎
FTC says that the derivative (rate of change) of the integral (accumulation) is the original function.↩︎
A linear algebra student might notice that the functions used for derivatives and integrals form transformations in the “vector space of smooth functions over the real numbers”—denoted C^∞(ℝ) —where functions are scalable by multiplication with r 𝜖 ℝ and additive with each other (the two axioms required for ) such that for 𝑓(x) = x there is r⋅𝑓(x) = r⋅x and 𝑓(x) + 𝑓(x) = x + x. Further, the derivatives are D: C^∞(ℝ) → C^∞(ℝ) and 𝑓 → d𝑓/dx and the kernel of this space where D: 𝑓 → 0 is the set of constant functions such that C 𝜖 {C₀ , C₁ , C₂ , …} in Figure 3 (Logan, Appendix B).↩︎
In an elementary algebra class, this means integration and differentiation share the same domain (possible input) and codomain (possible output), but integration has a restricted image (restricted output) —meaning differentiation is one-to-one, or categorically isomorphic, while integration is into or injective—categorically monomorphic (uses every input)—but not onto or surjective— categorically epimorphic (uses every output). In this way, CT can illuminate the relationship between the integral and the derivative.↩︎
Homology uses algebraic topology to label manifolds. In geometry, this looks like finding holes in shapes. In algebra, this requires many layers of abstraction.↩︎
Natural Transformation can be thought of as a morphism between functors.↩︎
The piecing apart of the goups fromed by the positive real numbers under multiplication is outlined by three sources (Holden, Karigala, and Samuel) in “Further Reading” (Appendix C)↩︎